This project tries to explain the differences in GDP per capita for different countries over time since 1960. I will look at how useful the Neo - Classical theory is for providing these explanations, by utilising its main assumption – that output depends only on quantities of relatively few inputs and technology. Thus, the fit of a regression of GDP levels against input levels in a suitable functional form would provide the first test for the explanatory power of neo-classical model.
Further tests come from additional assumptions of the neo-classical model. In particular, inputs should be paid their marginal product, and countries should converge to similar income levels, as marginal products of factors diminish to zero and technology diffuses.
However, finding evidence supporting neo-classical growth by no means implies that there are no better models available. Endogenous growth models are a large research area nowadays. I will look at some issues involved with simple AK endogenous models and conclude by briefly reviewing some modern endogenous growth research by Quah. The main issue in my project will be how to model the neo-classical growth model as precisely as possible. In particular I will have to use proxies for human capital and technological change to overcome data limitations. Due to space limitations, I will start off directly by incorporating the additions to the neo-classical model that have been added by recent research (Barro 1996, Mankiw et al 1996), without replicating.
The research is organised into six parts. After the introductory part, the second part solves the theoretical considerations of the neo-classical model, the third part describes the data used, and 4th part details the econometric techniques, 5th part the results. Sixth part goes on to explore the evidence from convergence, 7th part looks at extensions to on alternative growth models and limitations and part 7 concludes.
In this project I will mainly use the papers by Mankiw, Romer, Weil (1992) (MRW as they are popularly cited), Barro 1996 and Quah, however, extensions by Chung 1998 and Pesaran (1999) are also looked at. Most of the other quoted research comes from these sources and is quoted from them. I have also relied heavily on textbooks by Romer (Advanced Macroeconomics) and Barro and Sala-I-Martin (Economic Growth)
Neo-classical model presumes a simple competitive economy, where households own the inputs of the economy (capital and labor) and rent them to firms. Firms will pay them income, which they then choose to save or consume. Government, human capital and open economy can be added. The people also make choices as to how many children to have.
Firms hire labor, capital and other factors of production to determine the output levels. The choices of households are different in different countries, resulting in different availability of inputs and thus outputs.
Firms will use technology to create outputs from inputs. In particular, previous researchers (MRW) have found it useful to presume a specific production function (Cobb-Douglas) and technology function that is labor augmenting. I am not going to test the alternative neo-classical models.
The production function at time t can be then written as:
(1)
The notation is standard: Y is output, K is capital, L is labor and A
technology. It is assumed that there are only two inputs and they are paid their marginal
product (competitive economy). Also 
is a
constant, and neo-classical theory predicts that empirically it will be equivalent to the
factor’s share of GDP income. Furthermore, by restricting the factor shares to be
equal to 1, we assume constant returns to scale. This is a testable assumption. However,
when this test fails one has a problem with the neoclassical model, as increasing returns
would violate the competitive economy assumptions. Furthermore, neo-classical convergence
results require diminishing marginal products, and that is why a<1. If this is not the
case, endogenous growth model results. This is a testable assumption again.
The production function (PDF) in this form satisfies the Inada conditions. This also can be tested. In particular, this implies convergence of per capita income as the marginal products of capital and labor tend to 0.
L and A grow exogenously at rates n and g:
(2) 
(3) 
Thus, the number of effective units of labor A(t)L(t) grows at rate n+g.
The model assumes that constant fraction of output is invested (s).
Also there is a constant rate of depreciation 
. Thus the capital stock evolves as:
(4) 
It is helpful to express all quantities per effective unit of labor.
Thus I define k=K/AL, y=Y/AL. Furthermore, I will denote changes in a variable with a dot,
as is 
. Thus
(5) 
(6) 
Equation 6 implies that k(t) converges to a steady value k*
(7) 
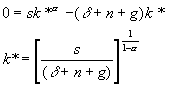
substituting 7 into 1 and taking logs yields
(8) 
This model is already testable. If we can find evidence of higher standard of living in countries with higher savings rate and lower population growth, then the Solow model is correct. It also predicts the magnitudes of the coefficients. Following MRW, I assume that growth of technology and depreciation are common across countries and will sum to 0.05. I will take on this point later and view some of the evidence presented by Pesaran (1999) how the convergence rates increase substantially when stochastic technology is used. I let the initial technology to vary according to a country and use number of parameters suggested by Barro (1996) as proxies.
As I will be dealing with a cross section of countries, the time subscripts can be omitted and the level of average technology as given. However, there will be a country specific error e. I will argue that this error is un-correlated with s and n, implying that savings rate and population growth are independent of the growth of per capita income. This is a crucial assumption for neo-classical growth. The alternative models where savings are determined endogenously, and possible test for the relationship between s and growth of GDP are viewed afterwards.
My basic economic testable model is:
(9) 
where a is the country specific initial technology level that will be proxied by numerous variables. I argue that the variables that determine income simultaneously determine changes in technology. Thus, the assumption that the residual technology is similar in all countries is not that restrictive
The second test I subject the data to is the convergence. Countries are not at their steady state. It will be possible to calculate from equation 9 the target or steady state level of income. If the income falls below that, then the country should grow faster. However, if it is above that then the country should grow slower. I will describe the theoretical convergence model briefly after the neoclassical growth model.
I will use Summers and Heston Penn World tables Mark 5.6 data set as my main source. However, much of the other variables were added from Barro and its sources are given in Barro (1996). I will use the 5-year averages of the data in order to filter out the temporary errors. In addition, many of the variables are only measured every 5 or 10 years, so shorter time periods are not practical. In particular I will choose the time period 1985-1992 as my initial cross-section and later try to confirm the results with earlier data. The period is long enough to deal with economic cycles and did not contain any major worldwide crises. I have excluded oil-producing countries because their incomes are determined too much by factors not related to standard inputs. In addition, former communist countries were excluded due to the unreliability of available data.
There are few missing observations that should not affect my results seriously. When they are related to the data only being available up to 1990, I have used the average of 1985-1990 instead. This should not introduce any systematic bias.
All data is available in downloadable format from my webpage http://www.ieg.ee/keith/stats. It also includes all the equations used and links to relevant references when they are available online.
I will estimate the equations by OLS, using instrumental and proxy variables where necessary. Although I have panel data available, I am specifically instructed to carry out cross-sectional analysis. I divided my data into three cross sectional groups. However, as the SUR method of using them as a system did not produce significantly better results, and as the three regressions separately where broadly similar, and I have severe space limitations only the last cross-section from 85-92 is reported.
I can use OLS because neo-classical growth theory predicts a linear relationship between the logs of the variables. However, in my extensions I will look at some of the work into endogenous growth models (convergence clubs) by Quah 1995 and others, which include non-linear estimation techniques. Furthermore, Pesaran (1999) has severely criticised the approach of using simple OLS with deterministic technology levels, and concludes that convergence rates can be as high as 15% a year when technology is allowed to be stochastic. However, the econometric techniques used in these papers are rather advanced and beyond this project.
Furthermore Romer 1989 (quoted from Barro 1996) shows that the measurement errors in GDP would bias the results. However, Barro has determined that the error would have to be substantial in regressions similar to mine to provide significant bias.
the key dependent variable I use is the Real GDP per capita in constant dollars adjusted for changes absorption and currency changes. ( RGDPTT80) There are numerous similar variables in Summers database, however, I think this is the most reasonable one for the model and is often used in other research. Changing the definition will not have substantial effects.
The other variables I use are (number at the end indicates the time period open85 applies to average of 85-92, G80 is average of 80-85). L as a first letter signifies log of the variable and D signifies change between two periods. More exact data description is on the webpage.
| G85 | Real Government share of GDP [%] (1985 intl. prices) Dependent variable |
| OPEN85 | Openness (Exports+Imports)/Nominal GDP |
| STLIV85 | Standard of Living Index (Consumption plus government consumption minus military expenditure, % of GDP) |
| asiae | Dummy for East Asian countries |
| laam | Dummy for Latin-American Countries. |
| safrica | Dummy for Sub-Saharan African countries. |
| human85 | Average schooling years in the total population over age 25 |
| lifee085 | Life expectancy at age 0 |
| gpop85 | Growth rate of population |
| pinstab80 | Measure of political instability. (0.5*Number of revolutions and coups per year + 0.5*Number of assassinations per million population per year) |
| bmp85l | Black market premium |
| LIFEE085 | life expectancy |
I will use lagged value of investment, because it takes time to build components of GDP. There are also problems in finding appropriate deflators for investment, which might show up in my research. Different values for human capital were tried and I selected the schooling years. I will use this because it signifies the stock of education as opposed to the flow, which as I show later is important distinction.
I will now present the results of estimations obtained by Microfit estimation package. I have largely used the testing down approach, over-specified the model and then eliminated the irrelevant variables.
First, equation 9.
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is LRGDPTT85
93 observations used for estimation from 1 to 93
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
C -.69921 .74133 -.94318[.348]
LI80 .83922 .10837 7.7442[.000]
LGPOPDEP85 -2.4827 .31511 -7.8788[.000]
*******************************************************************************
R-Squared .71119 R-Bar-Squared .70478
S.E. of Regression .57435 F-stat. F( 2, 90) 110.8139[.000]
Mean of Dependent Variable 8.0447 S.D. of Dependent Variable 1.0571
Residual Sum of Squares 29.6895 Equation Log-likelihood -78.8673
Akaike Info. Criterion -81.8673 Schwarz Bayesian Criterion -85.6662
DW-statistic 1.7924
*******************************************************************************
Diagnostic Tests
*******************************************************************************
* Test Statistics * LM Version * F Version *
* A:Serial Correlation*CHSQ( 1)= .98916[.320]*F( 1, 89)= .95679[.331]*
* B:Functional Form *CHSQ( 1)= 3.5613[.059]*F( 1, 89)= 3.5438[.063]*
* C:Normality *CHSQ( 2)= 2.7992[.247]* Not applicable *
* D:Heteroscedasticity*CHSQ( 1)= .0074040[.931]*F( 1, 91)= .0072453[.932]*
*******************************************************************************
A:Lagrange multiplier test of residual serial correlation
B:Ramsey's RESET test using the square of the fitted values
C:Based on a test of skewness and kurtosis of residuals
D:Based on the regression of squared residuals on squared fitted values
I will use the same diagnostics tests for all samples. I am not interested in the serial correlation, as one is dealing with a cross-section. The p-values of tests are in square brackets, and I will use a significance level of 10% for concern. Functional form is a RESET test and indicates the likely mis-specification of the equation, for example by including variables without taking logs first etc. It also indicates missed variables. Normality is mainly concerned with outliers in this context. Heteroscedasticity is going to be a main problem I suppose, as the countries are very different.
As seen the simple model without any technological modifications fits data quite well. There are slight problems with functional form and with normality, however, they are probably attributed to missing variables and outliers in the sample. Some countries are probably exceptionally small or with exceptionally low education, so that the tests for normality and functional form only marginally pass the 5% critical limit.
R2 of 0.71 indicates a good fit and is in line with results by Mankiw(1992) and others.
According to this equation 
. This is bigger than the average capital share of income (1/3), but is in
line with the broader measure of human capital.
In order to test for the constant rates of return I impose the constraint that coefficients of LI85 and LGPOPDEP have same magnitudes and opposite signs. I will use the functions of parameters test in Microfit (Wald test).
Analysis of Function(s) of Parameter(s)
*******************************************************************************
Based on OLS regression of LRGDPTT85 on:
C LI80 LGPOPDEP
93 observations used for estimation from 1 to 93
*******************************************************************************
Coefficients A1 to A3 are assigned to the above regressors respectively.
List of specified functional relationship(s):
F1 = A2 + A3
*******************************************************************************
Function Estimate Standard Error T-Ratio[Prob]
F1 -1.6435 .37647 -4.3655[.000]
*******************************************************************************
I will have to reject the hypotheses of equal magnitudes, indicating that there are possibly increasing returns to scale or that saving rate coefficient is biased because of the endogenous nature of the savings. However, it could also be that the initial level of technology is different in different countries and that affects the results. I can use education, life expectancy, political measures etc to account for the technology.
Including human capital is relatively straightforward. MRW have shown that when one looks the stock of human capital, then the relevant equation is:
(10) 
a is expected to be 1/3 as before, however, b, the share of human capital in output is harder to measure. MRW suggest that without human capital labor would be earning minimum wage, which is about 30-50% of real wage. Human capital is thus the other part, and if total human input is 2/3, human capital should lie between 1/3 or 4/9. Testing my equation 10:
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is LRGDPTT85
93 observations used for estimation from 1 to 93
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
C 4.5782 .83679 5.4712[.000]
LI80 .40584 .091456 4.4375[.000]
LGPODEP85 -.99542 .28231 -3.5260[.001]
LG85 -.39843 .12131 -3.2843[.001]
HUMAN85 .18704 .024676 7.5800[.000]
*******************************************************************************
R-Squared .85250 R-Bar-Squared .84580
S.E. of Regression .41509 F-stat. F( 4, 88) 127.1568[.000]
Mean of Dependent Variable 8.0447 S.D. of Dependent Variable 1.0571
Residual Sum of Squares 15.1627 Equation Log-likelihood -47.6213
Akaike Info. Criterion -52.6213 Schwarz Bayesian Criterion -58.9528
DW-statistic 1.5501
*******************************************************************************
Diagnostic Tests
*******************************************************************************
* Test Statistics * LM Version * F Version *
*******************************************************************************
* A:Serial Correlation*CHSQ( 1)= 4.6066[.032]*F( 1, 87)= 4.5340[.036]*
* B:Functional Form *CHSQ( 1)= .22379[.636]*F( 1, 87)= .20986[.648]*
* C:Normality *CHSQ( 2)= 2.2846[.319]* Not applicable *
* D:Heteroscedasticity*CHSQ( 1)= 3.9886[.046]*F( 1, 91)= 4.0777[.046]*
*******************************************************************************
A:Lagrange multiplier test of residual serial correlation
B:Ramsey's RESET test using the square of the fitted values
C:Based on a test of skewness and kurtosis of residuals
D:Based on the regression of squared residuals on squared fitted values
Adding the extra variable for human capital improves the results remarkably. R2 is now 0.85 indicating a very good fit, and most of the variables are significant. Increasing education by one year increases the log of GDP by roughly 16% from the mean level 3117 in 1985 dollars to 3732. There are problems with heteroscedasticity, however, the coefficients remain significant, even when White heteroscedasticity adjusted standard errors are used.
The variable for government is interesting as it reduces the income per capita significantly. The argument that Barro gives is that government consumption has no direct effect on private productivity, but lowered savings and growth through distortion from taxes. However, the Keynesian view would be radically different, and is rejected in this case. However, government provides most education in the country and that increases growth. The coefficient of government spending is about twice as big as the one on education. Government expenditure is about 19.7% of GDP on average. Therefore, if increasing government expenditure by 2% provides more than 0.4 years of extra education, it is a good thing. Similar calculations can be done for health etc.
Furthermore, I can now test the restriction that total physical capital and human capital coefficients are equivalent in magnitude to population growth and depreciation:
Analysis of Function(s) of Parameter(s)
*******************************************************************************
Based on OLS regression of LRGDPTT85 on:
C LI80 LGPODEP85 LG85 HUMAN85
93 observations used for estimation from 1 to 93
*******************************************************************************
Coefficients A1 to A5 are assigned to the above regressors respectively.
List of specified functional relationship(s):
F1=A2+A3+A5
*******************************************************************************
Function Estimate Standard Error T-Ratio[Prob]
F1 -.40254 .30826 -1.3059[.195]
This clearly supports the neoclassical growth model. With reasonable estimates of human capital and distortions to market economy, the model describes data very well.
Individually the coefficients are a= 0.28 and b= 0.16 which are broadly in line with my estimates. It is also clear that a+b<1 so there are diminishing returns. This is evidence against endogenous growth.
There are problems with heteroscedasticity, however, it is expected of cross-sectional data of such wide range. The model confirms constant returns to scale, and predicts capital share of output to be 0.40584/1.40584= 0.29 which is broadly consistent with the factors share of income in GDP.
I have not managed to use a consistent estimator for technology. R&D expenditures for these countries are not widely available. Furthermore, the diffusion of technology is a complicated process (Bernard and Jones). However, adding a variable for the openess of the economy to the regression (assuming most of the tecnological progress is through catch-up and copying not innovation) produces a coefficient of 0.0013389 with p value of 0.165, meaning that a country with 100% openness is growing about 1% a year faster than a country with 0% openness.
However, in order to be sure that this model actually explains growth in this crossection adequately, I will use dummies for different sections of the world to test whether they are significant. If they are that means the model has not explained some variables that differ significantly between these regions, but are not accounted for. One variable like this is probably social capital, that comes with culture and religion. However, the significance could also mean that there were initial differences between the groups before world trade and the diffusion of technology started, and these differences have percisted due to endogenous nature of the growth process.
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is LRGDPTT85
93 observations used for estimation from 1 to 93
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
C 6.7041 .88327 7.5901[.000]
LI80 .25997 .094255 2.7582[.007]
LGPODEP85 -.46467 .27769 -1.6733[.098]
LG85 -.47061 .11667 -4.0337[.000]
HUMAN85 .17843 .022637 7.8820[.000]
ASIAE -.52775 .16537 -3.1912[.002]
LAAM -.36245 .11028 -3.2866[.001]
SAFRICA -.56274 .14115 -3.9869[.000]
OPEN85 .0028082 .9712E-3 2.8916[.005]
*******************************************************************************
R-Squared .88501 R-Bar-Squared .87406
S.E. of Regression .37514 F-stat. F( 8, 84) 80.8114[.000]
Mean of Dependent Variable 8.0447 S.D. of Dependent Variable 1.0571
Residual Sum of Squares 11.8212 Equation Log-likelihood -36.0454
Akaike Info. Criterion -45.0454 Schwarz Bayesian Criterion -56.4421
DW-statistic 1.6751
*******************************************************************************
Diagnostic Tests
*******************************************************************************
* Test Statistics * LM Version * F Version *
*******************************************************************************
* A:Serial Correlation*CHSQ( 1)= 2.6145[.106]*F( 1, 83)= 2.4009[.125]*
* B:Functional Form *CHSQ( 1)= 1.1357[.287]*F( 1, 83)= 1.0262[.314]*
* C:Normality *CHSQ( 2)= .99293[.609]* Not applicable *
* D:Heteroscedasticity*CHSQ( 1)= 1.7079[.191]*F( 1, 91)= 1.7024[.195]*
*******************************************************************************
It is clear that the dummies are highly significant. In addition, adding them improves the regression results remarkably, eliminating heteroscedasticity. This suggests that there are important differences that were not accounted for before. Asian, South American and Saharan countries all have substantially lower GDP-s per capita than would otherwise be expected, with Latin - America doing better than the other two. However, the mean of the GDP per capita is 8.0447, thus a difference of 0.5 would imply GDP per capitas of 3117 and 1890 respectively in 1985 dollars. A difference of 40% which is not accounted by! Similar difference with Latin America is 25% (when using the higher number as base).
Another central assumption that can be tested from the data is the conditional convergence of the economies. The work on convergence is heavily based on (Barro 1996) and the main difference with the standard neo-classical model is that one is dealing with the growth rate of GDP per capita as the dependent variable, as opposed to just GDP per capita.
(11) 
where DY is the growth rate of Y, y is current GDP per capita and y* is the long-run GDP per capita. Neo-classical model assumes that the growth rate of y diminishes in y for given y* and rises in y* for given y. The target value, y* depends on an array of values, described by Barro 1996, but is broadly similar to the values defining the neo-classical model. Thus, if we include these variables, and thus estimate y* then if y is still significantly negatively affecting DY, we can conclude that there is conditional convergence.
MKW have provided formulae for calculating a priori estimated speeds of convergence. If convergence is linear:
(12) 
where l is speed of convergence, then l can be expressed as
(13) 
using the parameter values that I have estimated (the average growth rate of population in my sample is 0.025) then l=0.075*(1-0.28 -0.16)= 0.042 or 4%.
In the outset the countries are clearly not converging at absolute levels, and this promoted much of initial research into endogenous growth models (Romer 1987).
(World Bank website)
However, when one takes the changes in human capital into account, then the model can be fitted to data.
I have two sub-periods, 80-85 (RGDPTT80) and 85-92(RGDPTT80). Thus the average annual growth rate between these periods was:
DRGDPTT85=(log(RGDPTT80)-log(RGDPTT80))/6
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is DRGDPT85
93 observations used for estimation from 1 to 93
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
C .10391 .047941 2.1675[.033]
GPOP85 -.50658 .18704 -2.7084[.008]
LG85 -.010239 .0063108 -1.6225[.108]
HUMANM85 .2663E-3 .0015389 .17302[.863]
ASIAE .012205 .0076375 1.5981[.114]
LAAM -.028740 .0056737 -5.0655[.000]
SAFRICA -.012863 .0073530 -1.7493[.084]
BMP85L -.0083629 .0048633 -1.7196[.089]
LIFEE085 .0013678 .5478E-3 2.4971[.014]
LRGDPTT80 -.016367 .0054171 -3.0213[.003]
*******************************************************************************
R-Squared .56609 R-Bar-Squared .51904
S.E. of Regression .018665 F-stat. F( 9, 83) 12.0315[.000]
Mean of Dependent Variable .0079663 S.D. of Dependent Variable .026913
Residual Sum of Squares .028914 Equation Log-likelihood 243.5736
Akaike Info. Criterion 233.5736 Schwarz Bayesian Criterion 220.9106
DW-statistic 1.6564
*******************************************************************************
Diagnostic Tests
*******************************************************************************
* Test Statistics * LM Version * F Version *
*******************************************************************************
* * * *
* A:Serial Correlation*CHSQ( 1)= 2.6801[.102]*F( 1, 82)= 2.4332[.123]*
* * * *
* B:Functional Form *CHSQ( 1)= .29412[.588]*F( 1, 82)= .26015[.611]*
* * * *
* C:Normality *CHSQ( 2)= 6.4507[.040]* Not applicable *
* * * *
* D:Heteroscedasticity*CHSQ( 1)= .2956E-3[.986]*F( 1, 91)= .2893E-3[.986]*
The convergence coefficient is significant at 1.6% a year, indicating a half-life of 43 years. This is somewhat higher half-life than other calculations show. Also, the education levels are not significant in my regression. This might indicate that if one takes a longer time period then the educational levels will not reflect the growth potential of a country, and social capital, and other hardly observable variables might be more important. On the other hand it might indicate that education and fertility levels are highly correlated and thus already included. However, using just male education levels will not make the results more significant. However, black market and population growth significantly hinder the per capita growth of income, at the same time increase in life expectancy (can be thought of as a proxy for better healthcare etc) helps the growth rate. Furthermore, government expenditure has a negative effect on growth with a p value of 0.108.
It turns out that the country dummies are still significant, casting doubt on my results. However, repeating the exercise with a period from 80-85 yields similar results.
Graphically:
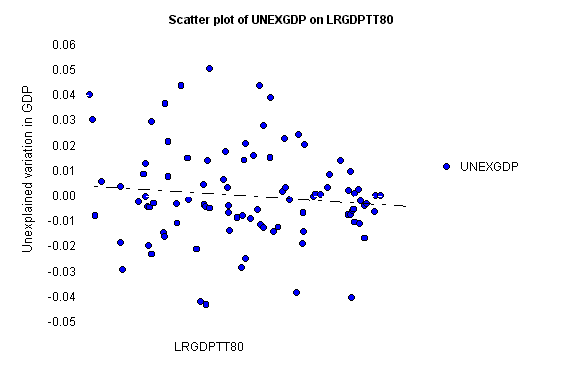This shows that
although there is some tendency for convergence, it does not really explain much of the
residual variation.
There is also much talk about 
convergence. However, this would require time series analysis, which I will
not carry out. Furthermore, Quah has done some Monte – Carlo studies showing that if
GDP follows a unit root then the convergence rate is biased and will be about 2% for
samples of 100. It does seem peculiar to me as well that 2% magical level is quoted
everywhere, and there could be a mechanical reason behind this. If there is and there is
no additional convergence, this would support the endogenous growth models that I describe
in the next section.
Failing to reject the classical growth models does not mean that they are correct. Few growth regressions never specify the alternative models the tests are supposed to discriminate against. Implicitly they claim to test the classical growth models versus the endogenous growth models. What are the powers of these tests? There is no a priori reason to suppose that the endogenous growth models do not also imply a negative partial correlation between initial income and subsequent growth for example, or that they necessarily imply increasing returns to scale.
Many of the endogenous models predict some convergence and are similar to the neo-classical model. However, in allowing the technological process to be internally generated, they might have a better explanatory and predictive capacity. Furthermore, they might be helpful in determining the direction of causation between components of the growth model, like answering whether investment causes growth or vice-versa, and might provide better policy recommendations.
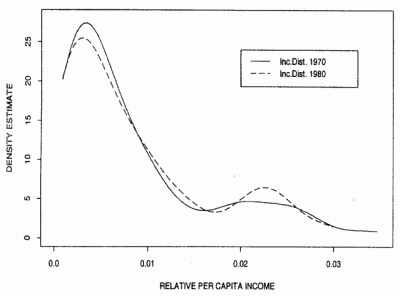
This graph illustrates a popular convergence club assumption where by countries will polarise. (Bianchi). Similar ideas involve poverty traps etc.
However, these ideas fail if one views policy choices as endogenous. Every country could adopt open trade policies, and if they choose to have military regime, they are not in a sense trapped to poverty.
Thus, it is not clear, whether endogenous models are better or worse than Neo - Classical. Neo-classical ones definitely manage to describe the data reasonably well, and the convergence hypothesis is supported by the data. However, they fail mostly in a dynamic setting that is not picked up by my cross-sectional model very well.
Barro, Robert J. (1991), "Economic Growth in a Cross Section of Countries" Quarterly Journal of Economcis 106(2): 407-443 http://www.jstor.ac.uk
Barro, Robert J. (1997), "Determinants of Economic Growth: A Cross-Country Empirical Study" Harvard Institute for International Development Discussion Paper #579. NBER working paper 5698 http://www.nber.org
Barro, Robert J. and Xavier Sala-i-Martin (1992), "Convergence" Journal of Political Economy 100(2): 223-251. http://www.jstor.ac.uk
Barro, Robert J. and Xavier Sala-i-Martin (1995), "Economic Growth"
Ben-David, Dan "Convergence Clubs and subsistence economies" NBER WP 6267 http://www.nber.org
Bianchi Journal of Applied Econometrics "Testing for Convergence" vol 12 1997
Chung "A lousy survey on Growth Empirics" 1998, webpage.Kim-Sau Chung's compilation of growth regressions
Mankiw, N. Gregory, David Romer and David N. Weil (1992), "A Contribution to the Empirics of Economic Growth" Quarterly Journal of Economics 107(2): 407-437. http://www.jstor.ac.uk
Pesaran, M. Hashem Stochastic Growth Models and Their Econometric Implications (webpage).Hashem Pesaran
Peasaran, M. Hashem Journal of Applied Econometrics "Growth and Convergence" vol 12 1997
Quah, Danny T. (1995), "Empirics for Growth and Convergence " 1995, webpage. Danny Tyson Quah, Professor of Economics
Quah, Danny T. (1995), " Convergence Empirics Accross economies with some capital mobility" 1995, webpage. Centre for Economic performance Discussion Paper. Danny Tyson Quah, Professor of Economics
Quah, Danny T. (1996), "Twin Peaks: Growth and Convergence in Models of Distribution Dynamics" Economic Journal 106(July): 1045-1055. Danny Tyson Quah, Professor of Economics
Romer, David "Advanced Macroeconomics" 1994.