

Let us look at the process of price determination and
output determination from the point of
view of a consumer who possesses a given bundle of goods, some of which he or she will wish to exchange with
others, rather than a consumer with a
given income. It is the decision to exchange which is of interest to us.
See Hildenbrand and Kirman, Intro to
Equilibrium Analysis, pp 1 12.
More generally, we must examine the relationship
between utility maximising choices and
the phenomenon of exchange in a competitive market which results in price and output determination (where
prices include wages and the rate of
interest, and determining the level of output includes determining
factor utilisation, in particular, the
level of employment). This allows us to try to
develop what is known as general equilibrium theory, in which the
interaction of all decision makers in
all markets is considered simultaneously, in the economy as a whole.
A famous article which presents general equilibrium theory in diagrams is F. Bator,/ "Simple analytics of welfare maximisation", AmerEcoReview (AER), 1957. Ignore the fact that the article is about welfare and concentrate on the way it shows how markets interact. A simple presentation of the structure of general equilibrium is available in the s standard textbooks. Then read the first four chapters of J.R.Hicks Value and Capital.- (Wicksteed, Eco Journal (Egg 1914 even argues that supply curves do not exist.)
In starting of this explanation I must make a couple of assumptions:
1. All possible bundles of goods can be finely divided
2. Domination does not exist
3. No negative goods exists, but consumers a capable of comparing them to their existing goods
4. People prefer mixes to extreme (convex indifference)
5. For now we take 2 goods A and B and 2 inputs L and D. The production functions A=fa(La,Da) and B=fb(Lb,Db)
There are also 2 consumers with utility functions Uy=fy(Ay,Ny), and Ux=fx(Ax,Nx)
With these simple assumptions an Edgeworth space of exchange can be constructed with only 2 goods and 2 consumers.

Initial indifference curves (initial utility) is given:
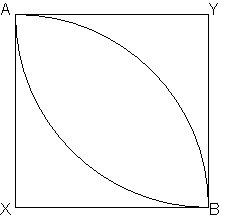
The shaded area forms a core, the place where Pareto improvements start to happen. Now people can see that by exchanging their goods they can reach to a higher utility level. The solution will essentially lie in the core:
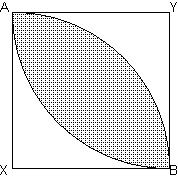
As seen there are many possible points where increasing one's utility can only be made by making the other one worse off. If there are more people and goods then more exchange can occur leading to a further improvement until all possible improvements are eliminated and a Pareto efficient equilibrium will occur. This would require many dimensional graphs so I will stick to 2 goods. The final effect will not depend on how much each of a good every person had before, they will still reach to the same competitive equilibrium.
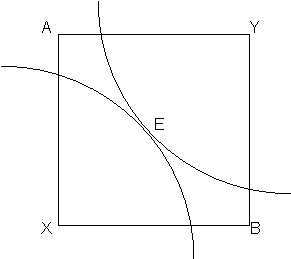
Decentralisation of prices will also occur as when prices are given and the utilities will not correspond people will soon discover that and exchange goods in different ration, thus equalising the price. However when markets are small some people might actually be better of by throwing some goods away (like was done in Brazil) in order to keep the price up and will still be better off.
The goods that people have can be their skills, capital, land or even entrepreneurship. This equilibrium reflects the case when a demand for on good from one consumer is exactly balanced by the supply of the same good from another consumer. The price is the loss of utility that must be compensated to the consumer for the trade to occur. As people value their last units very expensively, they have to gain large amount of utility from the other goods in order to give up last units. So their supply of the goods they possess is upward sloping and goes to vertical when they have depleted their sources. The utility they receive from other goods given to them diminishes as they have more of them, so demand for goods is downward sloping.
Now when the equilibriums with relatively different amounts of goods are drawn the contract curve can be modelled:
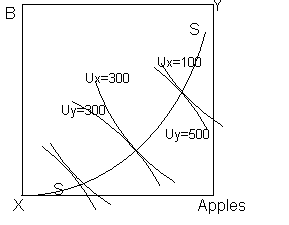
Note that when Uy<Ux it does not imply Uy is worse off or opposite.
Taking the supply side of goods. The production possibility functions (when land and labour are given) are:
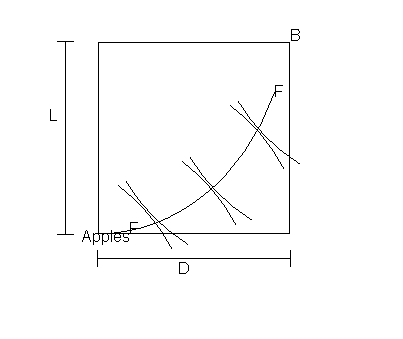
When the PPF for A and B are tangent a Pareto efficient equilibrium occurs as all the inputs have been used and there is no way of producing more of 1 without loosing the other.
An exchange efficiency locus FF and consists of the point of tangency between different PPFs. The locus of FF consists of points where in the production process MRS of labour = MRS land and will give us the efficient output of B on every output of A and the relative amounts of L and D employed in producing each one of these.
Changing the axes we have a PPF for A and B - when using all available L and D efficiently.
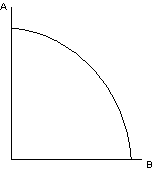
Its slope is the marginal rate of transformation. It indicates how much B can be produced by transferring L and D (while maintaining the MRS equal) from the production of A.
The exchange efficiency problem is to find a locus in the utility box that an increase in Ux would mean a reduction in Uy and so that all the L and D would be used (i.e. we are on a PPF line). The supply in this case is the PPF and demand SS line.
From the SS line we can draw a utility space showing possible utilities of X and Y:
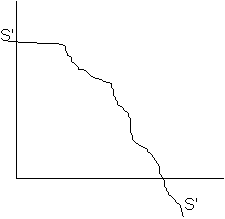
But as said before the MRS (the slope of PPF) shows how labour and land are associated, then the most utility can be achieved where the slope of PPF is equal to S'S' (highest possible value for S'S' and the slope(denoted by BB):
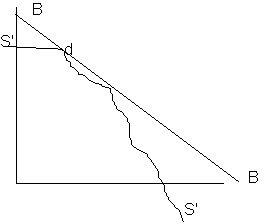
Several optima can always occur, in this case it is in d.
That is where the slopes of touching utility curves for X and Y are equal to the slope of PPF (most is produced and most utility achieved). In that case the number of goods defined by the production function is divided by X and Y as to get most utility.
In other words, BB curve is achieved when we move the utility box around underneath it and determine the point in core where Ux and Uy are tangent and this tangent is parallel to the tangent of PPF at the point where this box touches it:
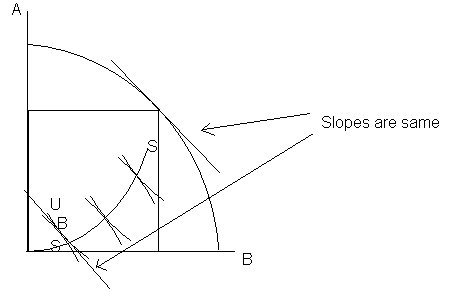
The different places of B in different boxes correspond to the equilibrium points. To get a single point we must examine ethical reasons (not in this essay).
If we now take the same slope on the isoquants touching on the FF line it will fix all variables and we have also an equilibrium point (see above graphs).
Now I will find prices of A and B and wage and rent. w and r will be allocated (from the profit max. assumption) so that MRS= (in fixed input prices). MRS is the eq. tangent to both isoquants of A and B. The price of goods will be comparable to the marginal utility derived from consuming them, so =. In this point ratio is also equal to the PPF slope, which is logical as prices should reflect the real cost. I did not include the standard MU stuff, the essay would be too long.
There is however a relationship between input rents and prices. As the firms are profit maximisers, in perfect competition they will hire until MPP of a factor = and we have our relationship from there. Third equation relating these 4 prices would be Eulers product exhaust theorem whereby all inputs would exhaust the income from selling them, thus wL+rD=paA+pnN, but we can't find a fourth equation, we can only express other 3 prices by knowing one of them. Nobody holds money in perfect world anyway, so only relative prices mater.
There is a much simpler approach to this by just considering the utility curves. Consumer tries to reach the highest utility curve possible, this will be tangent to PPF and at that point MRS=MRT:

If relative prices would be different to the slope of PP, then there would be either excess supply or demand, but the consumer will equate PP to its utility, if he can obtain that quantity from the market.
Last thing about interest rate. This is the price of capital. Investment can also be viewed in terms of PPF, instead of good B we use future consumption. Rate of return on investment determines the interest rate as projects with RoR above current interest only will go ahead, so more projects will be done at lower interest.
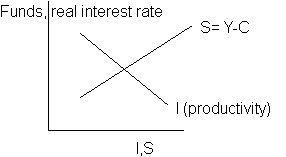
We assume that the real interest rate is the same as nominal(no inflation). This says that the lower the interest more money is demanded.
When excess of supply occurs the price falls, so the interest rate falls.
If the interest falls and less is invested
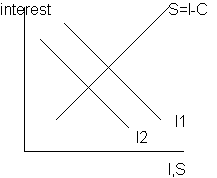
With the savings being as a supply of funds, the same way if interest is higher more is saved.
The prices of factors of production can be seen as an indirect exchange because you are not giving actual goods to a person that he makes, but a monetary value of the goods as a wage. So he can go and buy the same goods others have made and others buy his goods, final outcome will be like they would have exchanged the goods for their skills, only this was done indirectly, through the use of money. When people value the good that a person makes low, then the firm's MRP of that product will be lower, so he either employs the person for less hours or pays him less. So the utilities of other persons have indirectly, through a profit maximising entrepreneur in perfect knowledge determined the persons wage.